目录
- 面试题03:数组中重复的数字 (简单)
- 面试题04. 二维数组中的查找(简单)
- 面试题05. 替换空格(简单)
- 面试题06. 从尾到头打印链表(简单)
- 面试题07. 重建二叉树(中等)
- 面试题09. 用两个栈实现队列(简单)
- 面试题10- I. 斐波那契数(简单)
- 面试题10- II. 青蛙跳台阶问题(简单)
- 面试题11. 旋转数组的最小数字(简单)
- 面试题12. 矩阵中的路径(中等)
- 面试题13. 机器人的运动范围(中等)
- 面试题14- I. 剪绳子(中等)
- 面试题15. 二进制中1的个数(简单)
- 面试题16. 数值的整数次方(中等)
- 面试题17. 打印从1到最大的n位数(简单)
- 面试题18. 删除链表的节点(简单)
- 面试题20. 表示数值的字符串(中等)
- 面试题21. 调整数组顺序使奇数位于偶数前面(简单)
- 面试题22. 链表中倒数第k个节点(简单)
- 面试题24. 反转链表(简单)
- 面试题25. 合并两个排序的链表(简单)
- 面试题26. 树的子结构(中等)
- 面试题27. 二叉树的镜像(简单)
- 面试题28. 对称的二叉树(简单)
- 面试题29. 顺时针打印矩阵(简单)
- 面试题30. 包含min函数的栈(简单)
- 面试题31. 栈的压入、弹出序列(中等)
- 面试题32 - I. 从上到下打印二叉树(简单)
- 面试题32 - II. 从上到下打印二叉树 II(简单)
- 面试题32 - III. 从上到下打印二叉树 III(中等)
- 面试题33. 二叉搜索树的后序遍历序列(中等)
- 面试题34. 二叉树中和为某一值的路径(中等)
- 面试题35. 复杂链表的复制(中等)
- 面试题36. 二叉搜索树与双向链表(中等)
- 面试题37. 序列化二叉树(困难)
- 面试题38. 字符串的排列(中等)
- 面试题39. 数组中出现次数超过一半的数字(简单)
- 面试题40. 最小的k个数(简单)
- 面试题41. 数据流中的中位数(困难)
- 面试题42. 连续子数组的最大和(简单)
- 面试题43. 1~n整数中1出现的次数(中等)
- ()
面试题03:数组中重复的数字 (简单)
-
题目描述
找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
示例 1:
输入:
[2, 3, 1, 0, 2, 5, 3]
输出:2 或 3限制:
2 <= n <= 100000
-
解法
思路1:使用 HashSet 来进行处理,因为 HashSet 本身不允许出现重复元素,所以当添加元素失败或已经包含该数字时,则表示出现了重复元素,将其返回即可。时间复杂度:O(n),空间复杂度:O(n)
思路2:从题目描述中我们可以看出,因为所有数字都在 0 ~ n-1 的范围内,其实完全可以省掉额外的空间开辟,将每个位置的数交换映射到其对应的数组下标下面,当出现新的元素与其对应的下标中的数字相等时,即为重复数字。时间复杂度:O(n),空间复杂度:O(1)
-
代码
class Solution {
public int findRepeatNumber(int[] nums) {
Set<Integer> numsSet = new HashSet<>();
for(int num: nums) {
if(!numsSet.add(num)) {
return num;
}
}
return -1;
}
}
class Solution {
public int findRepeatNumber(int[] nums) {
for(int i=0;i<nums.length;i++){
while(i!=nums[i]){
if(nums[i]==nums[nums[i]]){
return nums[i];
}
int tmp = nums[i];
nums[i] = nums[tmp];//注意这里不能写成nums[i]=nums[nums[i]],会死循环
nums[tmp] = tmp;
}
}
return -1;
}
}
面试题04. 二维数组中的查找(简单)
-
题目描述
在一个 n * m 的二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
示例 1:
现有矩阵 matrix 如下:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]给定 target = 5,返回 true。
给定 target = 20,返回 false。
限制:
给定 target = 5,返回 true。
给定 target = 20,返回 false。 -
解法
从二维数组的右上角开始查找。如果当前元素等于目标值,则返回 true。如果当前元素大于目标值,则移到左边一列。如果当前元素小于目标值,则移到下边一行。
-
代码
class Solution {
public boolean findNumberIn2DArray(int[][] matrix, int target) {
int row = matrix.length;
if(matrix==null||row==0) return false;
int col = matrix[0].length;
int i=0,j=col-1;
while(i<row&&j>=0){
if(target==matrix[i][j]){
return true;
}else if(target>matrix[i][j]){
i++;
}else{
j--;
}
}
return false;
}
}
面试题05. 替换空格(简单)
-
题目描述
请实现一个函数,把字符串 s 中的每个空格替换成”%20”。
示例 1:
输入:s = “We are happy.”
输出:”We%20are%20happy.”限制:
0 <= s 的长度 <= 10000
-
解法
由于每次替换从 1 个字符变成 3 个字符,使用字符数组可方便地进行替换。建立字符数组地长度为 s 的长度的 3 倍,这样可保证字符数组可以容纳所有替换后的字符。
-
代码
class Solution {
public String replaceSpace(String s) {
int length = s.length();
char[] array = new char[length * 3];
int size = 0;
for (int i = 0; i < length; i++) {
char c = s.charAt(i);
if (c == ' ') {
array[size++] = '%';
array[size++] = '2';
array[size++] = '0';
} else {
array[size++] = c;
}
}
String newStr = new String(array, 0, size);
return newStr;
}
}
class Solution {
public String replaceSpace(String s) {
s=s.replaceAll(" ","%20");
return s;
}
}
面试题06. 从尾到头打印链表(简单)
-
题目描述
输入一个链表的头节点,从尾到头反过来返回每个节点的值(用数组返回)。
示例 1:
输入:head = [1,3,2]
输出:[2,3,1]限制:
0 <= 链表长度 <= 10000
-
解法
这题本身没难度,栈或者递归,第二个解法试了下stream,效率极低
-
代码
class Solution {
public int[] reversePrint(ListNode head) {
if(head==null) return new int[0];
ListNode node = head;
Stack<ListNode> stack = new Stack<>();
while(node!=null){
stack.push(node);
node = node.next;
}
int[] result = new int[stack.size()];
int i=0;
while(!stack.isEmpty()){
result[i++] = stack.pop().val;
}
return result;
}
}
class Solution {
ArrayList<Integer> list = new ArrayList<>();
public int[] reversePrint(ListNode head) {
if(head==null) return new int[0];
recur(head);
int[] result = list.stream().mapToInt(Integer::valueOf).toArray();
return result;
}
public void recur(ListNode tmp){
if(tmp.next!=null){
reversePrint(tmp.next);
}
list.add(tmp.val);
}
}
class Solution {
ArrayList<Integer> tmp = new ArrayList<Integer>();
public int[] reversePrint(ListNode head) {
recur(head);
int[] res = new int[tmp.size()];
for(int i = 0; i < res.length; i++)
res[i] = tmp.get(i);
return res;
}
void recur(ListNode head) {
if(head == null) return;
recur(head.next);
tmp.add(head.val);
}
}
非递归方式反转链表
public static Node reverseList(Node node) {
Node pre = null;
Node next = null;
while (node != null) {
next = node.next;
node.next = pre;
pre = node;
node = next;
}
return pre;
}
面试题07. 重建二叉树(中等)
-
题目描述
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例 1:
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]限制:
0 <= 节点个数 <= 5000
-
解法
前序得到根节点,去中序那得到根节点下标,左边是中序的左子树,右边是右子树,递归创建
-
代码
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder==null||preorder.length==0){
return null;
}
int rootNum = preorder[0];
TreeNode tmpNode = new TreeNode(rootNum);
int rootIndex = 0;
for(int i=0;i<inorder.length;i++){
if(rootNum==inorder[i]){
rootIndex = i;
}
}
int[] preorderLeft = Arrays.copyOfRange(preorder,1,1+rootIndex);
int[] inorderLeft = Arrays.copyOfRange(inorder,0,rootIndex);
int[] preorderRight = Arrays.copyOfRange(preorder,1+rootIndex,preorder.length);
int[] inorderRight = Arrays.copyOfRange(inorder,1+rootIndex,inorder.length);
tmpNode.left = buildTree(preorderLeft,inorderLeft);
tmpNode.right = buildTree(preorderRight,inorderRight);
return tmpNode;
}
}
面试题09. 用两个栈实现队列(简单)
-
题目描述
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
示例 1:
输入: [“CQueue”,”appendTail”,”deleteHead”,”deleteHead”]
[[],[3],[],[]]
输出:[null,null,3,-1]限制:
1 <= values <= 10000
最多会对 appendTail、deleteHead 进行 10000 次调用 -
解法
出栈前,判断一下,把一个栈扔到另外一个里
-
代码
class CQueue {
public Stack<Integer> stack1;
public Stack<Integer> stack2;
public CQueue() {
stack1 = new Stack<>();
stack2 = new Stack<>();
}
public void appendTail(int value) {
stack1.push(value);
}
public int deleteHead() {
if(!stack2.isEmpty()){
return stack2.pop();
}else if(stack1.isEmpty()){
return -1;
}else{
while(!stack1.isEmpty()){
stack2.push(stack1.pop());
}
return stack2.pop();
}
}
}
面试题10- I. 斐波那契数(简单)
-
题目描述
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项。斐波那契数列的定义如下:F(0) = 0, F(1) = 1 F(N) = F(N - 1) + F(N - 2), 其中 N > 1.答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 5
输出:5限制:
0 <= n <= 100
-
解法
注意斐波那契变种题即可
-
代码
class Solution {
public int fib(int n) {
if(n==0) return 0;
if(n==1) return 1;
int[] result = new int[n+1];
result[0]=0;
result[1]=1;
for(int i=2;i<n+1;i++){
result[i]=(result[i-1]+result[i-2])% 1000000007;
}
return result[n];
}
}
面试题10- II. 青蛙跳台阶问题(简单)
-
题目描述
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:2限制:
0 <= n <= 100
-
解法
斐波那契变种
-
代码
class Solution {
public int numWays(int n) {
if(n==0) return 1;
if(n==1) return 1;
if(n==2) return 2;
int a=1,b=2;
int result=0;
for(int i=3;i<n+1;i++){
result=(a+b)%1000000007;
a=b;
b=result;
}
return result;
}
}
面试题11. 旋转数组的最小数字(简单)
-
题目描述
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转,该数组的最小值为1。
示例 1:
输入:[3,4,5,1,2]
输出:1示例 2:
输入:[2,2,2,0,1]
输出:0 -
解法
二分法,重点!减治思想
用左边位置 left 和中间位置 mid 的值进行比较是否可以?
举例:[3, 4, 5, 1, 2] 与 [1, 2, 3, 4, 5] ,此时,中间位置的值都比左边大,但最小值一个在后面,一个在前面,因此这种做法不能有效地减治。用右边位置 right 和中间位置 mid 的值进行比较是否可以?
举例:[1, 2, 3, 4, 5]、[3, 4, 5, 1, 2]、[2, 3, 4, 5 ,1],用右边位置和中间位置的元素比较,可以进一步缩小搜索的范围。补充说明:遇到 nums[mid] == nums[right] 的时候,不能草率地下定结论最小数字在哪一边,但是可以确定的是,把 right 舍弃掉,并不影响结果。
-
代码
class Solution {
public int minArray(int[] numbers) {
int low=0;
int high=numbers.length-1;
int mid=0;
while(low<high){
mid=low+(high-low)/2;
if(numbers[mid]>numbers[high]){
low=mid+1;
}else if(numbers[mid]==numbers[high]){
high=high-1;
}else{
high=mid;
}
}
return numbers[low];
}
}
面试题12. 矩阵中的路径(中等)
-
题目描述
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。例如,在下面的3×4的矩阵中包含一条字符串“bfce”的路径(路径中的字母用加粗标出)。
[[“a”,”b”,”c”,”e”],
[”s”,”f”,”c”,”s”],
[“a”,”d”,”e”,”e”]]但矩阵中不包含字符串“abfb”的路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。
示例 1:
输入:board = [[“A”,”B”,”C”,”E”],[“S”,”F”,”C”,”S”],[“A”,”D”,”E”,”E”]], word = “ABCCED”
输出:true限制:
1 <= board.length <= 200
1 <= board[i].length <= 200 -
解法
解法1:路径问题一般需要visit来存储是否访问过,由于每个点都可以是起点,所以在两个for循环中使用回溯。在回溯内部,上下左右走是递归的入口,如果能走返回true
解法2:深度优先搜索(DFS)+ 剪枝 解决。
- 深度优先搜索: 可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归,先朝一个方向搜到底,再回溯至上个节点,沿另一个方向搜索,以此类推。
- 剪枝: 在搜索中,遇到 这条路不可能和目标字符串匹配成功 的情况(例如:此矩阵元素值和目标字符值不同、路径已访问此元素),则应立即返回,称之为 可行性剪枝 。
-
代码
class Solution {
boolean[] visited;
public boolean exist(char[][] board, String word) {
int row=board.length;
int col=board[0].length;
boolean result=false;
visited = new boolean[row*col];
for(int i=0;i<row;i++){
for(int j=0;j<col;j++){
result = result||existCore(board,i,j,word,0);
}
}
return result;
}
public boolean existCore(char[][] board,int row,int col,String word,int index){
int rowLen=board.length;
int colLen=board[0].length;
if(board[row][col]!=word.charAt(index)||visited[row*colLen+col]){
return false;
}
if(board[row][col]==word.charAt(index)&&index==word.length()-1){
return true;
}
visited[row*colLen+col]=true;
if(row>0&&existCore(board,row-1,col,word,index+1)) return true;
if(row<rowLen-1&&existCore(board,row+1,col,word,index+1)) return true;
if(col>0&&existCore(board,row,col-1,word,index+1)) return true;
if(col<colLen-1&&existCore(board,row,col+1,word,index+1)) return true;
visited[row*colLen+col]=false;
return false;
}
}
class Solution {
public boolean exist(char[][] board, String word) {
char[] words = word.toCharArray();
for(int i = 0; i < board.length; i++) {
for(int j = 0; j < board[0].length; j++) {
if(dfs(board, words, i, j, 0)) return true;
}
}
return false;
}
boolean dfs(char[][] board, char[] word, int i, int j, int k) {
if(i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != word[k]) return false;
if(k == word.length - 1) return true;
char tmp = board[i][j];
board[i][j] = '/';
boolean res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) ||
dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i , j - 1, k + 1);
board[i][j] = tmp;
return res;
}
}
面试题13. 机器人的运动范围(中等)
-
题目描述
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3限制:
1 <= n,m <= 100
0 <= k <= 20 -
解法
使用深度优先搜索(Depth First Search,DFS)方法进行求解。回溯是深度优先搜索的一种特例,它在一次搜索过程中需要设置一些本次搜索过程的局部状态,并在本次搜索结束之后清除状态。而普通的深度优先搜索并不需要使用这些局部状态,虽然还是有可能设置一些全局状态。
-
代码
public class Solution {
int result=0;
boolean[] visited = null;
public int movingCount(int threshold, int rows, int cols)
{
visited = new boolean[rows*cols];
countCore(threshold,rows,cols,0,0);
return result;
}
public void countCore(int threshold,int rows,int cols,int row,int col){
boolean judgeD=judgeDigit(threshold,row,col);
if(!judgeD||visited[row*cols+col]){
return;
}
result++;
visited[row*cols+col]=true;
if(row>0) countCore(threshold,rows,cols,row-1,col);
if(row<rows-1) countCore(threshold,rows,cols,row+1,col);
if(col>0) countCore(threshold,rows,cols,row,col-1);
if(col<cols-1) countCore(threshold,rows,cols,row,col+1);
}
public boolean judgeDigit(int threshold,int row,int col){
int count=0;
while(row>0){
count+=row%10;
row/=10;
}
while(col>0){
count+=col%10;
col/=10;
}
if(count>threshold){
return false;
}else{
return true;
}
}
}
面试题14- I. 剪绳子(中等)
-
题目描述
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m] 。请问 k[0]k[1]…*k[m] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
示例 1:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36限制:
2 <= n <= 58
-
解法
贪心规则:
- 最高优先级: 3 。把绳子尽可能切为多个长度为 3 的片段,留下的最后一段绳子的长度可能为 0,1,2 三种情况。
- 次高优先级: 2 。若最后一段绳子长度为 2,则保留,不再拆为 1+1 。
- 最低优先级: 1; 若最后一段绳子长度为 1;则应把最后的 3 + 1 替换为 2 + 2,因为 2×2>3×1
如果需要对结果取模运算,需要对每一步取模,不然会溢出
-
代码
class Solution {
public int cuttingRope(int n) {
if(n<=3) return n-1;
int a=n/3;
int b=n%3;
if(b==0) return (int)Math.pow(3,a);
if(b==1) return (int)Math.pow(3,a-1)*4;
return (int)Math.pow(3,a)*2;
}
}
class Solution {
public int cuttingRope(int n) {
if(n == 2) {
return 1;
}
if(n == 3){
return 2;
}
int mod = (int)1e9 + 7;
long res = 1;
while(n > 4) {
res *= 3;
res %= mod;
n -= 3;
}
return (int)(res * n % mod);
}
}
面试题15. 二进制中1的个数(简单)
-
题目描述
请实现一个函数,输入一个整数,输出该数二进制表示中 1 的个数。例如,把 9 表示成二进制是 1001,有 2 位是 1。因此,如果输入 9,则该函数输出 2。
示例 1:
输入:00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 ‘1’。示例 2:
输入:11111111111111111111111111111101
输出:31
解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 ‘1’。 -
解法
依次判断整数的每一位是否为 1 。
-
代码
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int count=0;
while(n!=0){
count+=(n&1);
n=n>>>1;//无符号右移,忽略符号位,空位都以0补齐
}
return count;
}
}
面试题16. 数值的整数次方(中等)
-
题目描述
实现函数double Power(double base, int exponent),求base的exponent次方。不得使用库函数,同时不需要考虑大数问题。
示例 1:
输入: 2.00000, 10
输出: 1024.00000限制:
-100.0 < x < 100.0
n 是 32 位有符号整数,其数值范围是 [−231, 231 − 1] 。 -
解法
要注意的一点是,虽然题目中告诉我们不需要考虑大数问题,但是给出的 n 可以取到 -2147483648−2147483648(整型负数的最小值),因此,在编码的时候,需要将 n 转换成 long 类型。因为abs(INT_MIN) 比 INT_MAX 大1, 所以不能直接用 -n
写法一:递归写法(分治思想)
写法二:非递归写法(将指数看成二进制数)把指数 n 做“二进制分解”,在底数不断自身乘以自身的过程中,将最终结果需要的部分保存下来。

-
代码
class Solution {
public double myPow(double x, int n) {
long N = n;
if(n<0){
x=1/x;
return myPow(x,-N);
}
return myPow(x,N);
}
public double myPow(double x,long N){
if(N==0||x==1) return 1.0;
// 根据指数是奇数还是偶数进行分类讨论
// 使用位运算的 与 运算符代替了求余数运算
if((N&1)==0){
double square = myPow(x,N>>>1);// 分治思想:分
return square*square;// 分治思想:合
}else{
double square = myPow(x,(N-1)>>>1);
return square*square*x;
}
}
}
class Solution {
public double myPow(double x, int n) {
long N = n;
if(n<0){
x=1/x;
N*=-1;
}
double result=1;
while(N>0){
if((N&1)==1){
result*=x;
}
x*=x;
N>>>=1;
}
return result;
}
}
面试题17. 打印从1到最大的n位数(简单)
-
题目描述
输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数 999。
示例 1:
输入: n = 1
输出: [1,2,3,4,5,6,7,8,9]说明:
用返回一个整数列表来代替打印
n 为正整数 -
代码
class Solution {
public int[] printNumbers(int n) {
int max=(int)Math.pow(10,n);
int[] result = new int[max-1];
for(int i=1;i<max;i++){
result[i-1]=i;
}
return result;
}
}
面试题18. 删除链表的节点(简单)
-
题目描述
给定单向链表的头指针和一个要删除的节点的值,定义一个函数删除该节点。
返回删除后的链表的头节点。
注意:此题对比原题有改动
示例 1:
输入: head = [4,5,1,9], val = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9.说明:
题目保证链表中节点的值互不相同
若使用 C 或 C++ 语言,你不需要 free 或 delete 被删除的节点 -
代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode deleteNode(ListNode head, int val) {
ListNode tmp = head;
if(head.val==val) return head.next;
while(tmp!=null){
if(tmp.next.val==val){
tmp.next=tmp.next.next;
break;
}
tmp=tmp.next;
}
return head;
}
}
面试题20. 表示数值的字符串(中等)
-
题目描述
请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串”+100”、”5e2”、”-123”、”3.1416”、”0123”及”-1E-16”都表示数值,但”12e”、”1a3.14”、”1.2.3”、”+-5”及”12e+5.4”都不是。
-
解法
1)A[.[B]][e EC] 2).B[e EC]; 其中,A、C是整数,B是正整数 -
代码
/*
核心: 有效数字的模式有两种:1)A[.[B]][e|EC] 2).B[e|EC]; 其中,A、C是整数,B是正整数
有A的话,有没有B都可以
没有A的话, 必须有B
*/
class Solution {
//扫描字符串时的索引
int i=0;
public boolean isNumber(String s) {
//input check
if(s==null || s.length()==0)
return false;
//去掉首尾的空字符
s = s.trim();
boolean A = scanInteger(s), B=false, C=false;
//判断是否有B; 使用索引时要确保索引不越界
if(i<s.length() && s.charAt(i)=='.'){
i++;
B = scanUnsignedInteger(s);
}
//判断是否有C
if(i<s.length() && (s.charAt(i)=='e' || s.charAt(i)=='E')){
i++;
C = scanInteger(s);
//如果存在e|E, 但是没有C, 说明不是数字
if(C==false)
return false;
}
//here, 说明C是合格的, 只需判断A和B的情况
//i必须扫描完整个字符串 && (A合格则B合不合格都可以, A不合格则B必须合格)
return i==s.length() && (A || B);
}
private boolean scanInteger(String s){
if(i<s.length() && (s.charAt(i)=='+' || s.charAt(i)=='-'))
i++;
return scanUnsignedInteger(s);
}
private boolean scanUnsignedInteger(String s){
//起始索引
int start = i;
while(i<s.length() && s.charAt(i)>='0' && s.charAt(i)<='9'){
i++;
}
//i>start说明扫描到了数字;
//i<=start说明没有扫描到数字, 此种情况说明要么start越界, 要么s.charAt(start)不是数字
return i > start;
}
}
面试题21. 调整数组顺序使奇数位于偶数前面(简单)
-
题目描述
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。
示例 1:
输入:nums = [1,2,3,4]
输出:[1,3,2,4]
注:[3,1,2,4] 也是正确的答案之一。限制:
1 <= nums.length <= 50000
1 <= nums[i] <= 10000 -
解法
头尾指针,指向排好的奇数和偶数
-
代码
class Solution {
public int[] exchange(int[] nums) {
int oddIndex=0;
int evenIndex=nums.length-1;
while(oddIndex<evenIndex){
if((nums[oddIndex]&1)==1){
oddIndex++;
}else{
swap(nums,oddIndex,evenIndex);
evenIndex--;
}
}
return nums;
}
public void swap(int[] nums,int i,int j){
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
面试题22. 链表中倒数第k个节点(简单)
-
题目描述
输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。例如,一个链表有6个节点,从头节点开始,它们的值依次是1、2、3、4、5、6。这个链表的倒数第3个节点是值为4的节点。
示例 1:
给定一个链表: 1->2->3->4->5, 和 k = 2.
返回链表 4->5. -
解法
快慢指针,快的先走k步
-
代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode getKthFromEnd(ListNode head, int k) {
ListNode preNode = head;
for(int i=0;i<k;i++){
preNode = preNode.next;
}
ListNode resNode = head;
while(preNode!=null){
preNode = preNode.next;
resNode = resNode.next;
}
return resNode;
}
}
面试题24. 反转链表(简单)
-
题目描述
定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。
示例 1:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL限制:
0 <= 节点个数 <= 5000
-
解法
循环,记录好上一个
-
代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
ListNode pre = null;
ListNode cur = head;
while(cur!=null){
ListNode next = cur.next;
cur.next = pre;
pre = cur;
cur = next;
}
return pre;
}
}
面试题25. 合并两个排序的链表(简单)
-
题目描述
输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。
示例 1:
输入:1->2->4, 1->3->4
输出:1->1->2->3->4->4限制:
0 <= 链表长度 <= 1000
-
解法
递归,值小的链表的下一个递归,并且往后走一个
循环,利用一下dummyNode即可
-
代码
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if(l1==null) return l2;
if(l2==null) return l1;
if(l1.val<l2.val){
l1.next = mergeTwoLists(l1.next,l2);
return l1;
}else{
l2.next = mergeTwoLists(l1,l2.next);
return l2;
}
}
}
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode(0), p = dummy;
while (l1 != null && l2 != null) {
if (l1.val < l2.val) {
p.next = l1;
l1 = l1.next;
} else {
p.next = l2;
l2 = l2.next;
}
p = p.next;
}
if (l1 != null) p.next = l1;
if (l2 != null) p.next = l2;
return dummy.next;
}
}
面试题26. 树的子结构(中等)
-
题目描述
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
示例 1:
输入:A = [1,2,3], B = [3,1]
输出:false示例 2:
输入:A = [3,4,5,1,2], B = [4,1]
输出:true -
解法
大的那棵树为进入条件,如果值相等,进子函数,不相等大的树进孩子节点遍历找入口
子函数,递归进左右节点,判断是否都一样
-
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isSubStructure(TreeNode A, TreeNode B) {
boolean result = false;
if(A!=null&&B!=null){
if(A.val==B.val){
result = equalTree(A,B);
}
if(!result){
result = isSubStructure(A.left,B);
}
if(!result){
result = isSubStructure(A.right,B);
}
}
return result;
}
public boolean equalTree(TreeNode A,TreeNode B){
if(B==null) return true;
if(A==null) return false;
if(A.val!=B.val){
return false;
}else{
return equalTree(A.left,B.left)&&equalTree(A.right,B.right);
}
}
}
面试题27. 二叉树的镜像(简单)
-
题目描述
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
示例 1:
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]限制:
0 <= 节点个数 <= 1000
-
解法
交换左右子树,然后递归进左右子树
-
代码
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if(root==null) return null;
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
if(root.left!=null){
mirrorTree(root.left);
}
if(root.right!=null){
mirrorTree(root.right);
}
return root;
}
}
面试题28. 对称的二叉树(简单)
-
题目描述
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的。
示例 1:
输入:root = [1,2,2,3,4,4,3]
输出:true限制:
0 <= 节点个数 <= 1000
-
解法
先判断空值的情况,如果不空判断值是否相等,递归进左右
-
代码
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root==null){
return true;
}
return judge(root.left,root.right);
}
public boolean judge(TreeNode node1,TreeNode node2){
if(node1==null&&node2==null) return true;
if(node1==null||node2==null) return false;
if(node1.val!=node2.val){
return false;
}else{
return judge(node1.left,node2.right)&&judge(node1.right,node2.left);
}
}
}
面试题29. 顺时针打印矩阵(简单)
-
题目描述
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]限制:
0 <= matrix.length <= 100
0 <= matrix[i].length <= 100 -
解法
算出来圈数之后按圈从左到右,从上到下,从右到左,从下到上打印
-
代码
class Solution {
public int[] spiralOrder(int[][] matrix) {
if(matrix==null||matrix.length==0) return new int[0];
int row = matrix.length;
int col = matrix[0].length;
int[] result = new int[row*col];
int resultIndex = 0;
int circle = Math.min(row,col)/2+1;
for(int i=0;i<circle;i++){
//从左到右打印
for(int j=i;j<col-i;j++){
result[resultIndex++] = matrix[i][j];
}
if(resultIndex==row*col) break;
//从上到下打印
for(int j=i+1;j<row-i;j++){
result[resultIndex++] = matrix[j][col-i-1];
}
if(resultIndex==row*col) break;
//从右到左打印
for(int j=i+1;j<col-i;j++){
result[resultIndex++] = matrix[row-i-1][col-j-1];
}
if(resultIndex==row*col) break;
//从下到上打印
for(int j=i+1;j<row-i-1;j++){
result[resultIndex++] = matrix[row-j-1][i];
}
if(resultIndex==row*col) break;
}
return result;
}
}
面试题30. 包含min函数的栈(简单)
-
题目描述
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
示例 1:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min(); –> 返回 -3.
minStack.pop();
minStack.top(); –> 返回 0.
minStack.min(); –> 返回 -2.限制:
各函数的调用总次数不超过 20000 次
-
解法
两个栈,一个栈正常用,另外一个栈压入最小值
-
代码
class MinStack {
Stack<Integer> stack;
Stack<Integer> minStack;
/** initialize your data structure here. */
public MinStack() {
stack = new Stack<>();
minStack = new Stack<>();
}
public void push(int x) {
stack.push(x);
if(minStack.isEmpty()){
minStack.push(x);
}else if(x<=minStack.peek()){
minStack.push(x);
}else if(x>minStack.peek()){
minStack.push(minStack.peek());
}
}
public void pop() {
stack.pop();
minStack.pop();
}
public int top() {
return stack.peek();
}
public int min() {
return minStack.peek();
}
}
面试题31. 栈的压入、弹出序列(中等)
-
题目描述
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1限制:
0 <= pushed.length == popped.length <= 1000
0 <= pushed[i], popped[i] < 1000
pushed 是 popped 的排列。 -
解法
for循环将push压栈,每次压入后看是否能pop
-
代码
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
Stack<Integer> stack = new Stack<>();
int j=0;
for(int i=0;i<pushed.length;i++){
stack.push(pushed[i]);
while(!stack.isEmpty()&&stack.peek()==popped[j]){
stack.pop();
j++;
}
}
if(stack.isEmpty()){
return true;
}else{
return false;
}
}
}
面试题32 - I. 从上到下打印二叉树(简单)
-
题目描述
从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
示例 1:
给定二叉树: [3,9,20,null,null,15,7],返回[3,9,20,15,7]
限制:
节点总数 <= 1000
-
解法
简单的层序遍历,队列即可
-
代码
class Solution {
public int[] levelOrder(TreeNode root) {
if(root==null) return new int[]{};
LinkedList<TreeNode> que = new LinkedList<>();
List<Integer> resultList = new ArrayList<>();
que.add(root);
while(!que.isEmpty()){
TreeNode tmp = que.pop();
resultList.add(tmp.val);
if(tmp.left!=null) que.add(tmp.left);
if(tmp.right!=null) que.add(tmp.right);
}
int[] result = new int[resultList.size()];
for(int i=0;i<resultList.size();i++){
result[i] = resultList.get(i);
}
return result;
}
}
面试题32 - II. 从上到下打印二叉树 II(简单)
-
题目描述
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。
-
解法
层序遍历,while中多一层for循环,每一层添加完后,记录一下队列的size,为for循环的次数
方法二,利用递归
-
代码
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
if(root==null) return new ArrayList<>();
LinkedList<TreeNode> que = new LinkedList<>();
List<List<Integer>> result = new ArrayList<>();
que.add(root);
int levelSize=0;
while(!que.isEmpty()){
List<Integer> tmp = new ArrayList();
levelSize = que.size();
for(int i=0;i<levelSize;i++){
TreeNode tmpNode = que.pop();
tmp.add(tmpNode.val);
if(tmpNode.left!=null) que.add(tmpNode.left);
if(tmpNode.right!=null) que.add(tmpNode.right);
}
result.add(tmp);
}
return result;
}
}
面试题32 - III. 从上到下打印二叉树 III(中等)
-
题目描述
请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
-
解法
方法一:利用两个栈
方法二:递归,最后按层反转
-
代码
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
if(root==null) return new ArrayList<>();
List<List<Integer>> result = new ArrayList<>();
Stack<TreeNode> stack1 = new Stack<>();
Stack<TreeNode> stack2 = new Stack<>();
stack1.add(root);
List<Integer> tmpResult = new ArrayList<>();
while(!stack1.isEmpty()||!stack2.isEmpty()){
while(!stack1.isEmpty()){
TreeNode tmpNode = stack1.pop();
tmpResult.add(tmpNode.val);
if(tmpNode.left!=null) stack2.add(tmpNode.left);
if(tmpNode.right!=null) stack2.add(tmpNode.right);
}
result.add(new ArrayList<>(tmpResult));
tmpResult.clear();
while(!stack2.isEmpty()){
TreeNode tmpNode = stack2.pop();
tmpResult.add(tmpNode.val);
if(tmpNode.right!=null) stack1.add(tmpNode.right);
if(tmpNode.left!=null) stack1.add(tmpNode.left);
}
if(tmpResult.size()!=0) result.add(new ArrayList<>(tmpResult));
tmpResult.clear();
}
return result;
}
}
class Solution {
List<List<Integer>> ref;
public List<List<Integer>> levelOrder(TreeNode root) {
ref = new ArrayList<>();
if(root == null) {
return ref;
}
helper(root, 0);
for(int i = 1; i < ref.size(); i += 2) {
Collections.reverse(ref.get(i));
}
return ref;
}
private void helper(TreeNode root, int cnt) {
if(root == null) {
return;
}
if(ref.size() <= cnt) {
ref.add(new ArrayList<>());
}
ref.get(cnt).add(root.val);
helper(root.left, cnt + 1);
helper(root.right, cnt + 1);
}
}
面试题33. 二叉搜索树的后序遍历序列(中等)
-
题目描述
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
示例 1:
输入: [1,6,3,2,5]
输出: false示例 2:
输入: [1,3,2,6,5]
输出: true -
解法
后序遍历的特点,最后一个数是根节点,左子树都比根节点小,右子树都比根节点大。利用二叉搜索树的这个特点,先找到根节点的左右子树分界点,之后判断右子树是否都大于根节点,不满足返回false。满足的话最后递归左右子树。
-
代码
class Solution {
public boolean verifyPostorder(int[] postorder) {
if(postorder==null||postorder.length==0) return true;
return verifyCore(postorder,0,postorder.length-1);
}
public boolean verifyCore(int[] postorder,int start,int root){
if(start>=root) return true;
int i=0;
for(i=start;i<root;i++){
if(postorder[i]>postorder[root]){
break;
}
}
for(int j=i;j<root;j++){
if(postorder[root]>postorder[j]){
return false;
}
}
return verifyCore(postorder,start,i-1)&&verifyCore(postorder,i,root-1);
}
}
面试题34. 二叉树中和为某一值的路径(中等)
-
题目描述
输入一棵二叉树和一个整数,打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。
示例 1:
限制:
节点总数 <= 10000
-
解法
递归+回溯,list存入节点,满足则加入结果,递归进左右,递归后剪枝。
-
代码
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> tmpRes = new ArrayList<>();
public List<List<Integer>> pathSum(TreeNode root, int sum) {
if(root==null) return res;
tmpRes.add(root.val);
if(root.left==null&&root.right==null&&root.val==sum){
res.add(new ArrayList<>(tmpRes));
}
pathSum(root.left,sum-root.val);
pathSum(root.right,sum-root.val);
tmpRes.remove(tmpRes.size()-1);
return res;
}
}
面试题35. 复杂链表的复制(中等)
-
题目描述
请实现 copyRandomList 函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。
示例 1:
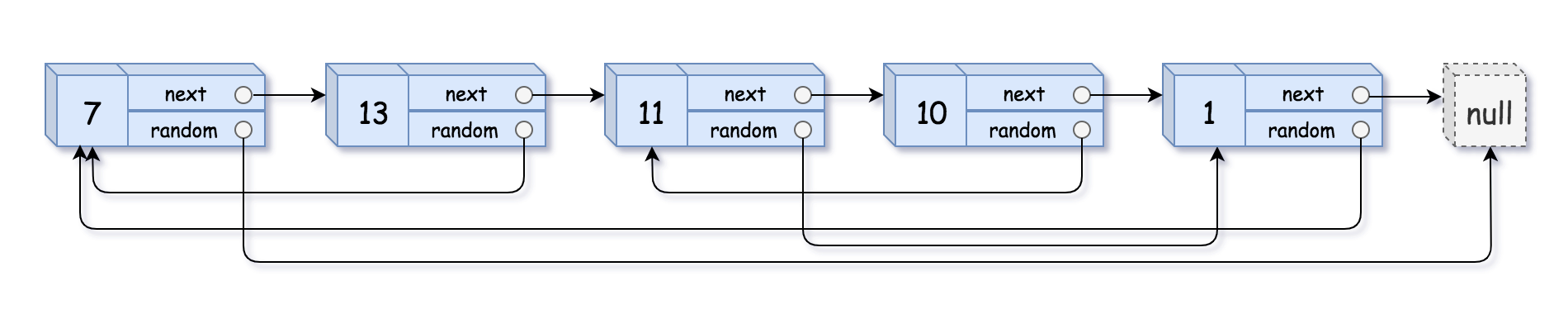
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]限制:
-10000 <= Node.val <= 10000
Node.random 为空(null)或指向链表中的节点。
节点数目不超过 1000 。 -
解法
第一遍,在原链表基础上每个节点后面复制一个节点。第二遍,连接上random。第三遍,把两个链表拆开。
-
代码
class Solution {
public Node copyRandomList(Node head) {
if(head==null) return null;
Node cur=head;
while(cur!=null){
Node copyNode = new Node(cur.val);
copyNode.next = cur.next;
cur.next = copyNode;
cur = cur.next.next;
}
cur=head;
while(cur!=null){
if(cur.random!=null){//注意这里的判空
cur.next.random = cur.random.next;
}
cur = cur.next.next;
}
cur=head;
Node res=cur.next;
while(cur!=null){
Node tmpNext = cur.next;
cur.next = cur.next.next;
if(tmpNext.next!=null){//注意这里的判空
tmpNext.next = tmpNext.next.next;
}
cur = cur.next;
}
return res;
}
}
面试题36. 二叉搜索树与双向链表(中等)
-
题目描述
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
示例 1:
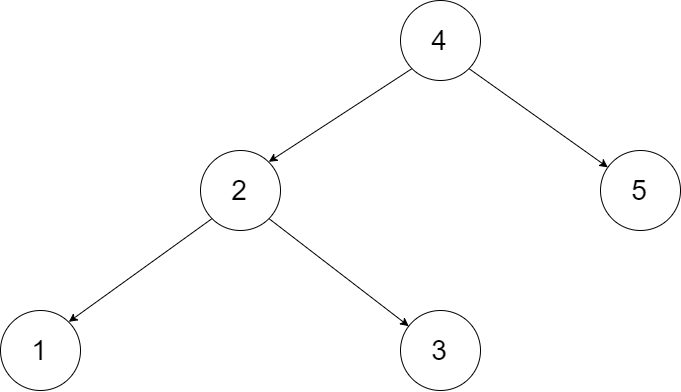
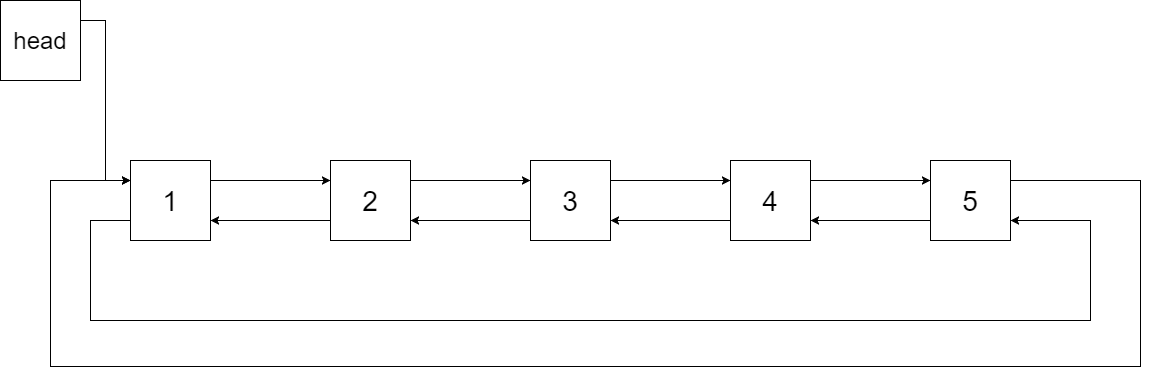
-
解法
方法一,先中序遍历一遍,然后改前后链接关系
-
代码
class Solution {
public Node treeToDoublyList(Node root) {
if(root==null) return null;
Stack<Node> stack = new Stack<>();
List<Node> order = new ArrayList<>();
Node cur = root;
while(cur!=null||!stack.isEmpty()){
if(cur!=null){
stack.push(cur);
cur=cur.left;
}else{
Node tmp=stack.pop();
order.add(tmp);
cur=tmp.right;
}
}
for(int i=1;i<order.size()-1;i++){
Node tmp=order.get(i);
tmp.left=order.get(i-1);
tmp.right=order.get(i+1);
}
order.get(0).left=order.get(order.size()-1);
if(order.size()>1){
order.get(0).right=order.get(1);
order.get(order.size()-1).left=order.get(order.size()-2);
}
order.get(order.size()-1).right=order.get(0);
return order.get(0);
}
}
如果不需要头尾相连的话:
public class Solution {
TreeNode head,pre=null;
public TreeNode Convert(TreeNode pRootOfTree) {
if(pRootOfTree==null) return null;
inOrder(pRootOfTree);
return head;
}
public void inOrder(TreeNode node){
if(node==null) return;
inOrder(node.left);
if(pre==null){
head=node;
}else{
pre.right=node;
}
node.left=pre;
pre=node;
inOrder(node.right);
}
}
头尾相连的遍历写法:(其实也可以不记录尾巴,和上面一样,只是这么看好看点罢了)
class Solution {
Node head=null,pre=null,tail=null;
public Node treeToDoublyList(Node root) {
if(root==null) return root;
//中序遍历访问节点并连接
inorder(root);
//连接头尾节点
head.left=tail;
tail.right=head;
return head;
}
private void inorder(Node root){
//递归出口
if(root==null) return ;
//访问左子树
inorder(root.left);
//将当前节点和上一个节点连接
if(pre==null) head=root;
else pre.right=root;
root.left=pre;
pre=root;
tail=root;
//访问右子树
inorder(root.right);
return ;
}
}
面试题37. 序列化二叉树(困难)
-
题目描述
请实现两个函数,分别用来序列化和反序列化二叉树。
-
解法
自己写的解法,序列化成string时,遇到空记录‘,#’,反序列化先按逗号分隔,之后判定#
-
代码
public class Codec {
// Encodes a tree to a single string.
String ser="";
public String serialize(TreeNode root) {
if(root==null) return null;
preOrder(root);
return ser;
}
public void preOrder(TreeNode node){
if(node==null){
ser+=",#";
return;
}
if(ser.length()==0||ser==null){
ser+=node.val;
}else{
ser+=","+node.val;
}
preOrder(node.left);
preOrder(node.right);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
if(data==null||data.length()==0) return null;
String[] node = data.split(",");
TreeNode root = dePreOrder(node);
return root;
}
int index=0;
public TreeNode dePreOrder(String[] node){
if(index>=node.length) return null;
if(node[index].equals("#")) return null;
int val = Integer.valueOf(node[index]);
TreeNode root = new TreeNode(val);
index++;
root.left = dePreOrder(node);
index++;
root.right = dePreOrder(node);
return root;
}
}
public class Codec {
// Encodes a tree to a single string.
int index=-1;
String serialize(TreeNode root) {
StringBuilder builder = new StringBuilder();
serializeHelper(root,builder);
return builder.toString();
}
void serializeHelper(TreeNode node,StringBuilder s){
if(node==null){
s.append("#,");
return;
}
s.append(node.val+",");
serializeHelper(node.left,s);
serializeHelper(node.right,s);
}
TreeNode deserialize(String str) {
if(str==null||str.equals("")){
return null;
}
String[] value = str.split(",");
return deserializeHelper(value);
}
TreeNode deserializeHelper(String[] value){
index++;
if(value[index].equals("#")){
return null;
}
TreeNode tmp = new TreeNode(Integer.parseInt(value[index]));
tmp.left = deserializeHelper(value);
tmp.right = deserializeHelper(value);
return tmp;
}
}
层序遍历方式:
public class Codec {
//很明显是一个层序遍历,
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if(root == null)return "[]";
String res = "[";
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
TreeNode cur = queue.poll();
if(cur!=null){
res+=cur.val+",";
queue.offer(cur.left);
queue.offer(cur.right);
}else{
res+="null,";
}
}
//去除最后的一个,
res = res.substring(0,res.length()-1);
return res+="]";
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
if(data == null || "[]".equals(data))return null;
String res = data.substring(1,data.length()-1);
String[] values = res.split(",");
int index = 0;
TreeNode head = generateTreeNode(values[index++]);
Queue<TreeNode> queue = new LinkedList<>();
TreeNode node = head;
queue.offer(head);
while(!queue.isEmpty()){
node = queue.poll();
node.left = generateTreeNode(values[index++]);
node.right = generateTreeNode(values[index++]);
if(node.left!=null){
queue.offer(node.left);
}
if(node.right!=null){
queue.offer(node.right);
}
}
return head;
}
public TreeNode generateTreeNode(String value){
if("null".equals(value))return null;
return new TreeNode(Integer.valueOf(value));
}
}
面试题38. 字符串的排列(中等)
-
题目描述
输入一个字符串,打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
示例 1:
输入:s = “abc”
输出:[“abc”,”acb”,”bac”,”bca”,”cab”,”cba”]限制:
1 <= s 的长度 <= 8
-
解法
经典全排列问题,回溯思想
题目类似于全排列。
这种题目基本上都是采用回溯的套路。
主要有几点需要注意:
1:for循环的起始位置。如果需要乱序,那么就是从0开始,如果每次都是顺序查找(不需要往前找),那么就需要有个start
2:标记数组。通过标记才能让递归后的代码知道之前用过哪些市局,就可以舍去这些数字。 -
代码
class Solution {
HashSet<String> set = new HashSet<>();
boolean[] visited;
StringBuilder sb = new StringBuilder();
public String[] permutation(String s) {
char[] ss = s.toCharArray();
Arrays.sort(ss);//可有可无
visited = new boolean[ss.length];
generate(ss,0);
String[] res = set.toArray(new String[0]);
return res;
}
public void generate(char[] ss,int index){
if(index==ss.length){
set.add(sb.toString());
}
for(int i=0;i<ss.length;i++){
if(!visited[i]){
sb.append(ss[i]);
visited[i]=true;
generate(ss,index+1);
visited[i]=false;
sb.deleteCharAt(index);
}
}
}
}
class Solution {
Set<String> result = new HashSet<>();
public String[] permutation(String s) {
if(s == null) return new String[]{};
boolean[] visited = new boolean[s.length()];
process(s, "", visited);
return result.toArray(new String[result.size()]);
}
private void process(String s, String letter, boolean[] visted){
if(s.length() == letter.length()){
result.add(letter);
return;
}
for(int i = 0; i < s.length(); i++){
char temp = s.charAt(i);
if(visted[i]) continue;
visted[i] = true;
process(s, letter + String.valueOf(temp), visted);
visted[i] = false;
}
}
}
面试题39. 数组中出现次数超过一半的数字(简单)
-
题目描述
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
示例 1:
输入: [1, 2, 3, 2, 2, 2, 5, 4, 2]
输出: 2限制:
1 <= 数组长度 <= 50000
-
解法
记录当前最多的那个数,一样+1,不一样-1,到0换数
-
代码
class Solution {
public int majorityElement(int[] nums) {
int resultCount=0;
int resultNum=nums[0];
for(int i=0;i<nums.length;i++){
if(nums[i]==resultNum){
resultCount++;
}else{
resultCount--;
if(resultCount==0){
resultNum=nums[i];
resultCount=1;
}
}
}
return resultNum;
}
}
面试题40. 最小的k个数(简单)
-
题目描述
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
示例 1:
输入:arr = [3,2,1], k = 2
输出:[1,2] 或者 [2,1]限制:
0 <= k <= arr.length <= 10000
0 <= arr[i] <= 10000 -
解法
方法一:快排思想,找到下标就可以停止了
方法二:优先队列往里面加
方法三:先创建一个大小为10001的数组line(随便起的名字),默认值是0不用管。遍历arr,每次将arr[i]的值作为line的下标,然后line[arr[i]]++。这样遍历完后,line这个数组存放的就是arr中每个值存放的次数。如arr=[3,2,1]。那么最后line=[0,1,1,1,0.,0..],又如arr=[0,1,2,1],则line=[1,2,1,0….]这样再遍历一次arr就可以了
-
代码
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
quickSort(arr,0,arr.length-1,k);
int[] res = Arrays.copyOfRange(arr,0,k);
return res;
}
public void quickSort(int[] arr,int low,int high,int k){
if(low>high) return;
int index = getIndex(arr,low,high);
if(index==k-1){
return;
}else{
quickSort(arr,low,index-1,k);
quickSort(arr,index+1,high,k);
}
}
public int getIndex(int[] arr,int low,int high){
int tmp=arr[low];
while(low<high){
while(low<high&&arr[high]>=tmp){
high--;
}
arr[low]=arr[high];
while(low<high&&arr[low]<=tmp){
low++;
}
arr[high]=arr[low];
}
arr[low]=tmp;
return low;
}
}
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if(k == 0) {
return new int[0];
}
Queue<Integer> queue = new PriorityQueue<>((a, b) -> (b - a));
for(int i: arr) {
if(queue.size() < k) {
queue.add(i);
} else {
if(queue.peek() > i) {
queue.remove();
queue.add(i);
}
}
}
int[] ref = new int[k];
int cnt = 0;
while(queue.size() > 0) {
ref[cnt++] = queue.remove();
}
return ref;
}
}
面试题41. 数据流中的中位数(困难)
-
题目描述
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
- void addNum(int num) - 从数据流中添加一个整数到数据结构中。
- double findMedian() - 返回目前所有元素的中位数。
示例 1:
输入:
[“MedianFinder”,”addNum”,”addNum”,”findMedian”,”addNum”,”findMedian”]
[[],[1],[2],[],[3],[]]
输出:[null,null,null,1.50000,null,2.00000]限制:
最多会对 addNum、findMedia进行 50000 次调用。
-
解法
分成两半,一个大顶堆,一个小顶堆
-
代码
class MedianFinder {
PriorityQueue<Integer> minHeap = null;
PriorityQueue<Integer> maxHeap = null;
/** initialize your data structure here. */
public MedianFinder() {
minHeap = new PriorityQueue<Integer>((a, b)->(a-b));
maxHeap = new PriorityQueue<Integer>((a,b)->(b-a));
}
int message=0;
public void addNum(int num) {
if((message&1)==1){
maxHeap.add(num);
minHeap.add(maxHeap.poll());
}else{
minHeap.add(num);
maxHeap.add(minHeap.poll());
}
message++;
}
public double findMedian() {
if(minHeap.size()>maxHeap.size()){
return minHeap.peek();
}else if(minHeap.size()==maxHeap.size()){
return (double)(maxHeap.peek()+minHeap.peek())/2;
}else{
return maxHeap.peek();
}
}
}
class MedianFinder {
private PriorityQueue<Integer> maxHeap, minHeap;
public MedianFinder() {
maxHeap = new PriorityQueue<>(Collections.reverseOrder());
minHeap = new PriorityQueue<>();
}
public void addNum(int num) {
maxHeap.offer(num);
minHeap.offer(maxHeap.poll());
//如果不平衡则调整
if (minHeap.size() > maxHeap.size()) {
maxHeap.offer(minHeap.poll());
}
}
public double findMedian() {
if (maxHeap.size() == minHeap.size()) {
return (maxHeap.peek() + minHeap.peek()) * 0.5;
}
return maxHeap.peek();
}
}
面试题42. 连续子数组的最大和(简单)
-
题目描述
输入一个整型数组,数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
示例 1:
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。限制:
1 <= arr.length <= 10^5
-100 <= arr[i] <= 100 -
解法
累加值,如果小于当前的被加数,则中间结果设置为被加数
-
代码
class Solution {
public int maxSubArray(int[] nums) {
int tmp=nums[0];
int result=nums[0];
for(int i=1;i<nums.length;i++){
if(tmp+nums[i]<nums[i]){
tmp=nums[i];
}else{
tmp+=nums[i];
}
result=Math.max(result,tmp);
}
return result;
}
}
class Solution {
public int maxSubArray(int[] nums) {
int ans = Integer.MIN_VALUE, sum = 0;
for(int num : nums) {
sum = Math.max(sum + num, num);
ans = Math.max(ans, sum);
}
return ans;
}
}
面试题43. 1~n整数中1出现的次数(中等)
-
题目描述
输入一个整数 n ,求1~n这n个整数的十进制表示中1出现的次数。
例如,输入12,1~12这些整数中包含1 的数字有1、10、11和12,1一共出现了5次。
示例 1:
输入:n = 12
输出:5限制:
1 <= n < 2^31
-
解法
暴力解法会超时,需要判断最高位是否为1,然后递归,找到递推公式(规律)很重要
-
代码
class Solution {
public int countDigitOne(int n) {
return dfs(n);
}
private int dfs(int n) {
if (n <= 0) {
return 0;
}
String numStr = String.valueOf(n);
int high = numStr.charAt(0) - '0';
int pow = (int) Math.pow(10, numStr.length() - 1);
int last = n - high * pow;
if (high == 1) {
// 最高位是1,如1234, 此时pow = 1000,那么结果由以下三部分构成:
// (1) dfs(pow - 1)代表[0,999]中1的个数;
// (2) dfs(last)代表234中1出现的个数;
// (3) last+1代表固定高位1有多少种情况。
return dfs(pow - 1) + dfs(last) + last + 1;
} else {
// 最高位不为1,如2234,那么结果也分成以下三部分构成:
// (1) pow代表固定高位1,有多少种情况;
// (2) high * dfs(pow - 1)代表999以内和1999以内低三位1出现的个数;
// (3) dfs(last)同上。
return pow + high * dfs(pow - 1) + dfs(last);
}
}
}
()
-
题目描述
示例 1:
限制:
-
解法
-
代码
